A thought experiment is a proposal for an experiment that would test or illuminate a hypothesis, theory, or principle. Given the structure of the proposed experiment, it may or may not be possible to actually perform the experiment and, in the case that it is possible for the experiment to be performed, no intention of any kind to actually perform the experiment in question may exist. The common goal of a thought experiment is to explore the potential consequences of the principle in question.
10. Simulated Reality

Simulated reality is the proposition that reality could be simulated—perhaps by computer simulation—to a degree indistinguishable from “true” reality. It could contain conscious minds which may or may not be fully aware that they are living inside a simulation. In its strongest form, the “simulation hypothesis” claims it is entirely possible and even probable that we are living in a simulated reality. This is quite different from the current, technologically achievable concept of virtual reality. Virtual reality is easily distinguished from the experience of “true” reality; participants are never in doubt about the nature of what they experience. Simulated reality, by contrast, would be hard or impossible to separate from “true” reality. In brain-computer interface simulations, each participant enters from outside, directly connecting their brain to the simulation computer. The computer transmits sensory data to the participant, reads and responds to their desires and actions in return; in this manner they interact with the simulated world and receive feedback from it. The participant may be induced by any number of possible means to forget, temporarily or otherwise, that they are inside a virtual realm (e.g. “passing through the veil”). While inside the simulation, the participant’s consciousness is represented by an avatar, which can look very different from the participant’s actual appearance. A dream could be considered a type of simulation capable of fooling someone who is asleep. As a result the “dream hypothesis” cannot be ruled out, although it has been argued that common sense and considerations of simplicity rule against it. One of the first philosophers to question the distinction between reality and dreams was Zhuangzi, a Chinese philosopher from the 4th Century BC.
9. Bell’s Spaceship Paradox

Bell’s spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. In Bell’s version of the this thought experiment, two spaceships, which are initially at rest in some common inertial reference frame, are connected by a taut string. At time zero in the common inertial frame, both spaceships start to accelerate, such that they remain a fixed distance apart as viewed from the rest frame. Question: Does the string break (i.e. does the distance between the two spaceships increase)? According to discussions by Dewan & Beran and also Bell, in the spaceship launcher’s reference frame the distance between the ships will remain constant while the elastic limit of the string is length contracted, so that at a certain point in time the string should break. Objections and counter-objections have been published to the above analysis. For example, Paul Nawrocki suggests that the string should not break. However we know the theory of relativity by Einstein which states if speed approaches near to that of light, distance should increase i.e it should break. According to Bell, a “clear consensus” of the CERN theory division arrived at the answer that the string would not break. Bell goes on to add, “Of course, many people who get the wrong answer at first get the right answer on further reflection”. Later, Matsuda and Kinoshita reported receiving much criticism after publishing an article on their independently rediscovered version of the paradox in a Japanese journal.
8. Infinite Monkey Theorem

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare. In this context, “almost surely” is a mathematical term with a precise meaning, and the “monkey” is not an actual monkey, but a metaphor for an abstract device that produces a random sequence of letters ad infinitum. The theorem illustrates the perils of reasoning about infinity by imagining a vast but finite number, and vice versa. The probability of a monkey exactly typing a complete work such as Shakespeare’s Hamlet is so tiny that the chance of it occurring during a period of time of the order of the age of the universe is minuscule, but not zero. Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. Popular interest in the typing monkeys is sustained by numerous appearances in literature, television, radio, music, and the Internet. In 2003, an experiment was performed with six Celebes Crested Macaques. Their literary contribution was five pages consisting largely of the letter ‘S’. There is a straightforward proof of this theorem. If two events are statistically independent, then the probability of both happening equals the product of the probabilities of each one happening independently.
Suppose the typewriter has 50 keys, and the word to be typed is banana. If we assume that the keys are pressed randomly and independently, then the chance that the first letter typed is ‘b’ is 1/50, and the chance that the second letter typed is a is also 1/50, and so on, because events are independent. Therefore, the chance of the first six letters matching banana is (1/50) × (1/50) × (1/50) × (1/50) × (1/50) × (1/50) = (1/50)6, less than one in 15 billion.
7. Galileo’s Balls
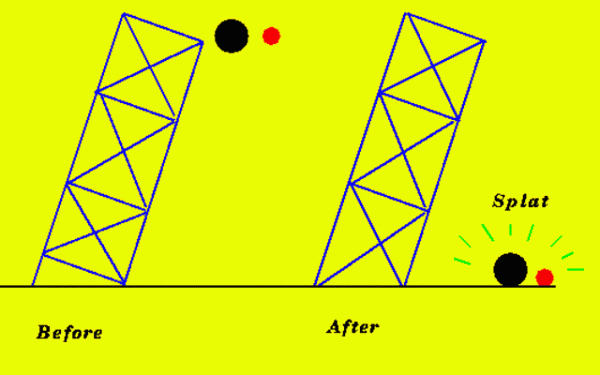
Contrary to what your teachers told you, Galileo Galilei likely did not drop balls from the Tower of Pisa; he conducted the gravity experiment in the laboratory of his mind. His 16th-century peers believed heavier objects fell faster than light ones. So Galileo imagined a heavy ball attached by a string to a light ball. According to Aristotelian logic, if a light object and a heavy object were tied together and dropped off a tower, then the heavier object would fall faster, and the rope between the two would become taut. This would allow the lighter object to create drag and slow the heavy one down. But Galileo reasoned that once this occurs, the weight of the two objects together should be heavier than the weight of either one by itself. Would the light ball create drag and slow the heavy one down? Nope, he concluded, they would hit the ground simultaneously.
6. Halting Problem

In computability theory, the halting problem is a decision problem which can be stated as follows: given a description of a program, decide whether the program finishes running or will run forever. This is equivalent to the problem of deciding, given a program and an input, whether the program will eventually halt when run with that input, or will run forever. Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist. We say that the halting problem is undecidable over Turing machines. B. Jack Copeland (2004) attributes the actual term halting problem to Martin Davis.
5. Doomsday Argument

The Doomsday argument ( DA ) is a probabilistic argument that claims to predict the number of future members of the human species given only an estimate of the total number of humans born so far. Simply put, it says that supposing the humans alive today are in a random place in the whole human history timeline, chances are we are about halfway through it. Denoting by N the total number of humans who were ever or will ever be born, the Copernican principle suggests that humans are equally likely (along with the other N − 1 humans) to find themselves at any position n, so humans assume that our fractional position f = n/N is uniformly distributed on the interval (0, 1] prior to learning our absolute position. If we take that 60 billion humans have been born so far (Leslie’s figure), then we can estimate that there is a 95% chance that the total number of humans N will be less than 20 × 60 billion = 1.2 trillion. Assuming that the world population stabilizes at 10 billion and a life expectancy of 80 years, it can be estimated that the remaining 1140 billion humans will be born in 9120 years. Depending on the projection of world population in the forthcoming centuries, estimates may vary, but the main point of the argument is that it is unlikely that more than 1.2 trillion humans will ever live.
4. Brain in a Vat

There has been no more influential thought experiment than the so-called “ brain in a vat ” hypothesis, which has permeated everything from cognitive science and philosophy to popular culture. The experiment asks you to imagine a mad scientist has taken your brain from your body and placed it in a vat of some kind of life sustaining fluid. Electrodes have been connected to your brain, and these are connected to a computer that generates images and sensations. Since all your information about the world is filtered through the brain, this computer would have the ability to simulate your everyday experience. If this were indeed possible, how could you ever truly prove that the world around you was real, and not just a simulation generated by a computer? If you’re thinking this all sounds a bit like The Matrix, you’re right. That film, along with several other sci-fi stories and movies, was heavily influenced by the brain in a vat thought experiment. At its heart, the exercise asks you to question the nature of experience, and to consider what it really means to be human.
3. Balls and Vase Problem

The Ross–Littlewood paradox (also known as the balls and vase problem or the ping pong ball problem ) is a hypothetical problem in abstract mathematics and logic designed to illustrate the seemingly paradoxical, or at least non-intuitive, nature of infinity. More specifically, the Ross–Littlewood paradox tries to illustrate the conceptual difficulties with the notion of a supertask, in which one is trying to complete an infinite number of tasks sequentially. The problem starts with an empty vase and an infinite supply of balls. One then performs an infinite number of steps, where at each step balls are added as well as removed from the vase. The question is then posed: How many balls are in the vase when one is done?
To complete an infinite number of steps, let us assume that the vase is empty at two minutes before noon, and that one performs the steps as follows:
- The first step is performed at one minute before noon.
- The second step is performed at 30 seconds before noon.
- The third step is performed at 15 seconds before noon.
- Each subsequent step n is performed at 21−n minutes before noon.
This guarantees that a countably infinite number of steps is performed by noon. At each step, 10 balls are added to the vase, and one ball is removed from the vase. The question now is: How many balls are in the vase at noon? Answers to the puzzle fall into 4l categories. 1) The most intuitive answer seems to be that the vase contains an infinite number of balls by noon. 2) However, suppose that the balls of the infinite supply of balls were numbered, and that at step 1 one inserts balls 1 through 10 into the vase, and removes ball number 1. At step 2, one inserts balls 11 through 20, and removes ball 2. This means that by noon, every ball n that is inserted into the vase is eventually removed in a subsequent step (namely, step n). Hence, the vase is empty at noon. 3) Although the state of the balls and the vase is well-defined at every moment in time prior to noon, no conclusion can be made about any moment in time at or after noon. Thus, for all we know, at noon, the vase just magically disappears. 4) The problem is ill-posed. To be precise, according to the problem statement, an infinite number of operations will be performed before noon, and then asks us about the state of affairs at noon. But, if infinitely many operations have to take place (sequentially) before noon, then noon is a point in time that can never be reached.
2. Schrödinger’s Cat
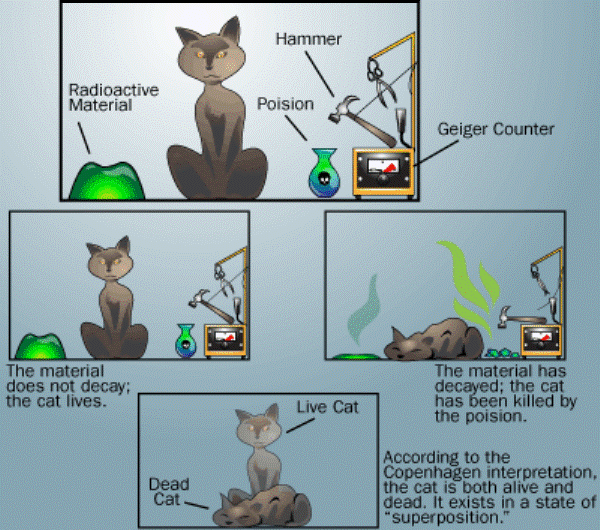
Schrödinger’s cat is a thought experiment, often described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The thought experiment presents a cat that might be alive or dead, depending on an earlier random event. A cat is trapped in a box with radioactive material, a Geiger counter, and a mechanism rigged to release poison if particle decay is detected. According to Erwin Schrödinger, the cat exists in two probable states. But that doesn’t track with reality (cats are not both alive and dead). Proposed in 1935, the postulate illustrates that some quantum concepts just don’t work at nonquantum scales. Also that Schrödinger was a dog person.
1. Maxwell’s Demon
Maxwell’s demon is a thought experiment created by the Scottish physicist James Clerk Maxwell, in which a supernatural being is instructed to attempt to violate the second law of thermodynamics. The second law of thermodynamics ensures (through statistical probability) that two bodies of different temperature, when brought into contact with each other and isolated from the rest of the Universe, will evolve to a thermodynamic equilibrium in which both bodies have approximately the same temperature. The thought experiment demonstrates Maxwell’s point by describing how to violate the 2nd Law to “show that the 2nd Law of Thermodynamics has only a statistical certainty.” In the experiment an imaginary container is divided into two parts by an insulated wall, with a door that can be opened and closed by what came to be called ” Maxwell’s Demon“. The hypothetical demon is able to let only the “hot” molecules of gas flow through to a favored side of the chamber, causing that side to appear to spontaneously heat up while the other side cools down.